| 摘要 | 包装材料的阻隔性能,在食品包装和药品包装中起着十分重要的作用。对于材料透气性能的检测,压差法是使用时间最久、使用范围最广的一种测试方法。随着测试技术和高精度压力计的发展,压差法大大地得到了改善。但是,对这种方法的疑问一直存在。认为压差会影响膜的结构,从而影响阻隔性。为了搞清这个问题,本文根据我们的实际测试数据,对压差和隔阻性的关系进行了探讨。 |
|---|---|
| 关键字 | 压差,阻隔性,透气性,塑料薄膜,包装 |
| 文档 | 点击查看PDF文档 |
包装材料的阻隔性能,在食品包装和药品包装中起着十分重要的作用。阻隔性能包括透气性能和透湿性能,测试方法多种多样。对于材料透气性能的检测,压差法是使用时间最久、使用范围最广的一种测试方法。但是,对压差法的测试数据存在一些质疑,其中之一是[1]:在测试过程中,由于材料的两侧存在着压差,这会破坏某些较为脆弱的材料的结构,产生小的裂纹、针孔等缺陷;还会使材料产生形变,厚度变薄,透气面积增大,从而影响实验结果。特别是当等压法在美国开始使用后,人们对这些因素的担忧更加严重。究竟压差法中压差的存在对材料透气性能有无影响?由此测得的透气量等数据,是否可靠?这个问题一直没有具体的数据来说明。因此,我们就此问题进行了大量的试验,以期得到明确清晰的结论。
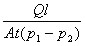 (2)
(2)1 透过率TR(Transmission Rate):单位时间内在单位面积上透过样品的测试气体总量Q;表示为:Q/(A t)
2 透气量R(Permeance):单位时间内,在单位分压差的作用下,在单位面积上透过样品的测试气体总量Q;表示为:Q/(A t△p)
三个量之间满足如下关系:

图1 VAC-V1气体渗透测试仪
材料(厚度 μm) | 分压差 (kPa) | ||||||
30 | 50 | 70 | 90 | 110 | 130 | 150 | |
PE (40) | 1875.43 | 3154.45 | 4391.56 | 6071.05 | 7204.33 | 8418.80 | 9919.87 |
CPP (40) | 1045.74 | 1763.57 | 2416.90 | 3010.48 | 3642.43 | 4437.63 | 5029.70 |
OPP (38) | 526.69 | 922.04 | 1332.30 | 1686.89 | 2032.81 | 2344.06 | 2718.35 |
PC (125) | 177.01 | 299.86 | 415.44 | 546.37 | 662.45 | 782.83 | 908.68 |
PC (175) | 123.61 | 217.15 | 306.77 | 398.42 | 489.72 | 584.72 | 664.50 |
PET (12) | 42.64 | 68.56 | 96.50 | 122.45 | 158.16 | 187.90 | 218.34 |
PET (23) | 23.18 | 38.16 | 53.82 | 69.16 | 82.35 | 97.41 | 109.71 |
PET (25) | 20.43 | 33.87 | 47.30 | 67.56 | 75.28 | 90.68 | 102.88 |
PET (70) | 8.45 | 13.18 | 18.28 | 23.64 | 29.67 | 34.26 | 39.20 |
PA (35) | 10.12 | 16.10 | 22.75 | 28.12 | 32.95 | 39.29 | 44.65 |
PE-EVOH-PE (55) | 1.29 | 1.45 | 1.75 | 1.79 | 2.07 | 2.60 | |
PA-PE (80) | 27.95 | 48.47 | 66.03 | 86.97 | 107.92 | 128.9 | 149.5 |
材料(厚度 μm) | 分压差 (kPa) | ||||||
30 | 50 | 70 | 90 | 110 | 130 | 150 | |
PE (40) | 6251.45 | 6308.90 | 6273.67 | 6745.61 | 6549.39 | 6476.79 | 6613.25 |
CPP (40) | 3406.16 | 3487.85 | 3375.64 | 3310.01 | 3285.18 | 3417.68 | 3431.51 |
OPP (38) | 1774.76 | 1818.71 | 1901.35 | 1860.38 | 1831.37 | 1793.22 | 1837.20 |
PC (125) | 590.01 | 599.72 | 593.48 | 590.07 | 604.99 | 602.84 | 607.98 |
PC (175) | 412.02 | 434.29 | 438.24 | 442.69 | 445.20 | 449.79 | 443.73 |
PET (12) | 142.14 | 137.65 | 136.77 | 136.18 | 143.47 | 145.96 | 145.56 |
PET (23) | 75.28 | 77.98 | 75.37 | 75.07 | 74.66 | 75.17 | 74.48 |
PET (25) | 68.10 | 67.74 | 67.57 | 67.28 | 67.10 | 69.76 | 68.59 |
PET (70) | 28.18 | 26.35 | 26.12 | 26.27 | 26.97 | 26.35 | 26.13 |
PA (35) | 33.68 | 32.22 | 32.04 | 31.24 | 29.70 | 30.75 | 30.69 |
PE-EVOH-PE (55) | 2.57 | 2.07 | 1.94 | 1.63 | 1.59 | 1.73 | |
PA-PE (80) | 94.30 | 94.57 | 92.22 | 96.34 | 97.80 | 100.21 | 101.99 |
材料(厚度 μm) | 分压差 (kPa) | ||||||
30 | 50 | 70 | 90 | 110 | 130 | 150 | |
PE (40) | 38.1 | 38.4 | 38.2 | 41.1 | 40.0 | 41.1 | 40.3 |
CPP (40) | 20.8 | 21.2 | 20.6 | 20.2 | 19.8 | 20.8 | 20.9 |
OPP (38) | 10.3 | 10.5 | 11.0 | 10.8 | 10.6 | 10.4 | 10.6 |
PC (125) | 11.2 | 11.4 | 11.3 | 11.2 | 11.5 | 11.5 | 11.6 |
PC (175) | 11.0 | 11.5 | 11.7 | 11.8 | 11.9 | 12.0 | 11.8 |
PET (12) | 0.260 | 0.252 | 0.250 | 0.249 | 0.262 | 0.267 | 0.266 |
PET (23) | 0.264 | 0.273 | 0.264 | 0.263 | 0.262 | 0.263 | 0.261 |
PET (25) | 0.259 | 0.258 | 0.257 | 0.256 | 0.256 | 0.266 | 0.261 |
PET (70) | 0.30 | 0.28 | 0.278 | 0.280 | 0.287 | 0.281 | 0.279 |
PA (35) | 0.180 | 0.172 | 0.171 | 0.167 | 0.158 | 0.164 | 0.164 |
PE-EVOH-PE (55) | 0.0215 | 0.0174 | 0.0163 | 0.0137 | 0.0132 | 0.0145 | |
PA-PE (80) | 1.15 | 1.15 | 1.12 | 1.17 | 1.19 | 1.22 | 1.24 |
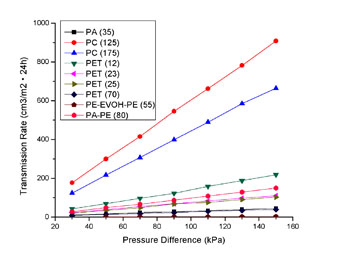
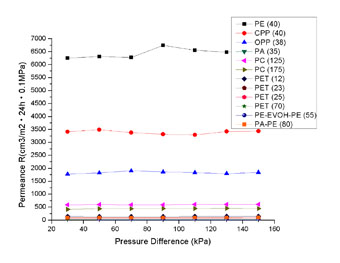
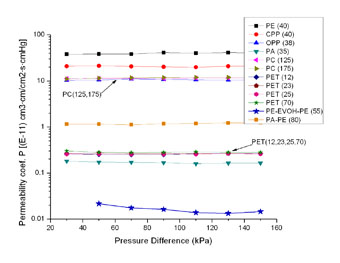
根据第一节的基本原理,透过率TR是单位时间透过单位面积的气体的量(重量或体积量)。这个量应该由两个因素决定:
1)材料本身的透气性能;
2)材料两边气体的浓度差。
如果材料本身的透气性能不变,那么,材料两边气体的浓度差越大,越有利于气体从高浓度向低浓度扩散。也就是TR会随着材料两边气体的浓度差增加而增加。从(1)式中可知,TR也就会随材料两边分压差的增加而增加。这也正是我们实验证明的一个结果。但是如果我们只关心材料本身的透气性能,就需要去掉这个材料外部的因素,即除去这个分压差,这也就有了(3)式中的透气量R。实验数据也证明了R(从而P)与分压差无关。这好比一个电路当中,如果一个固定电阻两端的电压差越大,流过这个固定电阻的电流就会越大。但不论这个电流多大,只要不会烧毁固定电阻,电阻的阻值都是不会变的。


 济南兰光新闻中心包含公司动态、公告、产品新闻等多种模块,为您展示最新、最全的企业资讯,让您了解更多包装检测行业的最新技术。
济南兰光新闻中心包含公司动态、公告、产品新闻等多种模块,为您展示最新、最全的企业资讯,让您了解更多包装检测行业的最新技术。 Labthink兰光拥有完善的服务体系,百余人的专业服务团队,能以多种语言通过电话、网络、移动平台、现场等多种途径为全球用户提供真诚、专业、及时、持续的服务和技术支持。
Labthink兰光拥有完善的服务体系,百余人的专业服务团队,能以多种语言通过电话、网络、移动平台、现场等多种途径为全球用户提供真诚、专业、及时、持续的服务和技术支持。